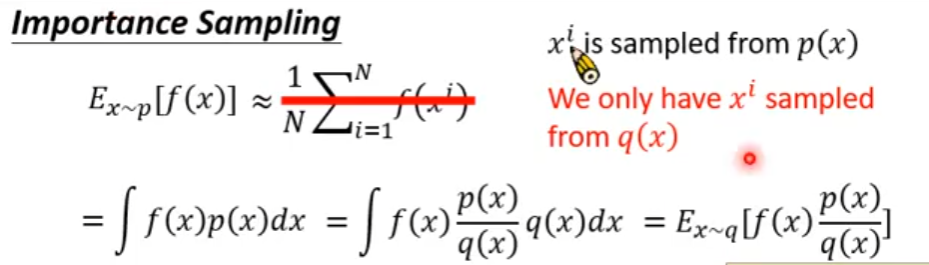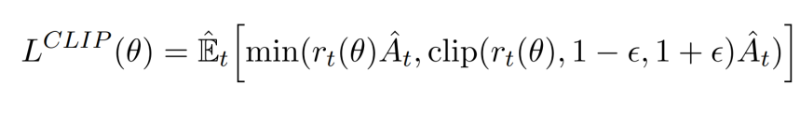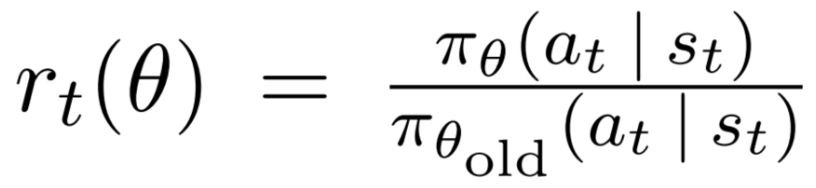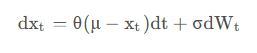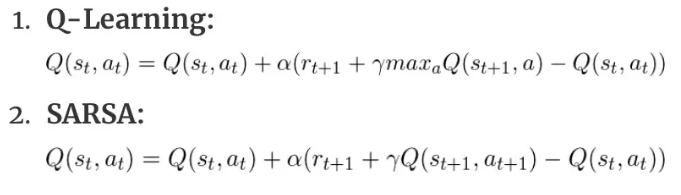Reinforce-Learning
clipped surrogate loss in PPO
PPO是一种off policy的强化学习算法,它的优势就是可以重复使用之前policy与环境交互得到的数据,它通过将一个分布中的采样数据转换为从另一个分布中的采样数据,即从old policy这个分布转换为new policy这个分布
PPO就是在此基础上做了进一步优化使得其能适应强化学习的环境,其核心就是下面这个公式:
其中的 ( r_t(θ) \ ) 为:
即新旧策略在状态St下得到at的概率比值,显然,如果该比值大于1,说明新的策略更倾向于选择该action
以下为 stable-baseline3 中该表达式的实现,其中,ratio就是上述的那个比值,clip_range取值为0.2
# clipped surrogate loss
policy_loss_1 = advantages * ratio
policy_loss_2 = advantages * th.clamp(ratio, 1 - clip_range, 1 + clip_range)
policy_loss = -th.min(policy_loss_1, policy_loss_2).mean()
现在就有两个问题,1)对clamp(clip)的理解,2)对min的理解
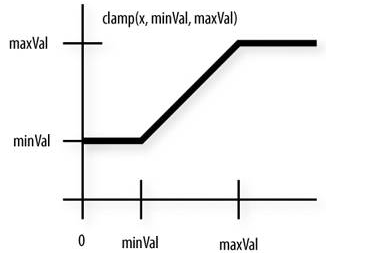
clamp
从公式中看出,clamp是对ratio的裁切,即避免它过大或过小,为什么要这么做呢?通过 Importance Sampling 的式子可以看出,将一个分布转换为另一个分布后,它的期望值是没变的,但是它们的方差是不同的,若仅采样有限数据,很容易出现误差
注意到上图中,两者方差的第一项是不同的,后者会多乘这个ratio。理论上来说,由于均值不受影响,所以只要采样的数据足够多,也不会对最终结果产生较大影响,但对于一个实际意义的马尔可夫奖励过程,几乎是不太可能采样足够多的
一个非常需要注意的点是,被clamp过的部分是没有梯度的,即梯度为0,根据链式求导法则,前面计算的梯度应该都是0
换句话说,我们并不希望new policy和old policy的差异过大,如果太大的话,干脆就不对模型做更新了
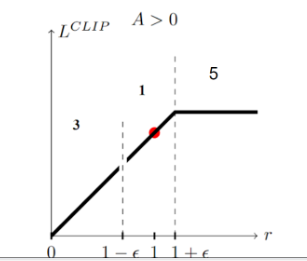
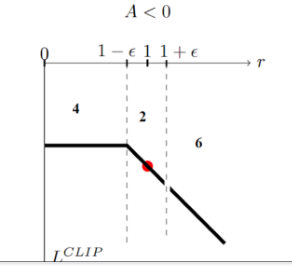
min
如果当前的Advantage是正值时,如果当前的new policy远小于(两者比值小于某个阈值)old policy得到该action的probability,我仍然希望模型能够学到东西(参数更新,增大policy取得该action的概率)。
相反,若此时,new policy的probability远大于old policy,因为此时advantage是正值,我们的目的就是要让new policy的probability更大,而它此时已经比old大了,所以我们就应该避免它更大,故此时反而应该将其clamp掉,使得其梯度为0,进而使其不做更新
如果当前的advantage是负值时,若new policy的probability远大于old policy,则继续让其更新,因为我们要试图减小policy产生该action的概率,反之亦然
参考
https://huggingface.co/learn/deep-rl-course/unit8/clipped-surrogate-objective
https://huggingface.co/learn/deep-rl-course/unit8/visualize
stable-baselines3中的SAC
现象
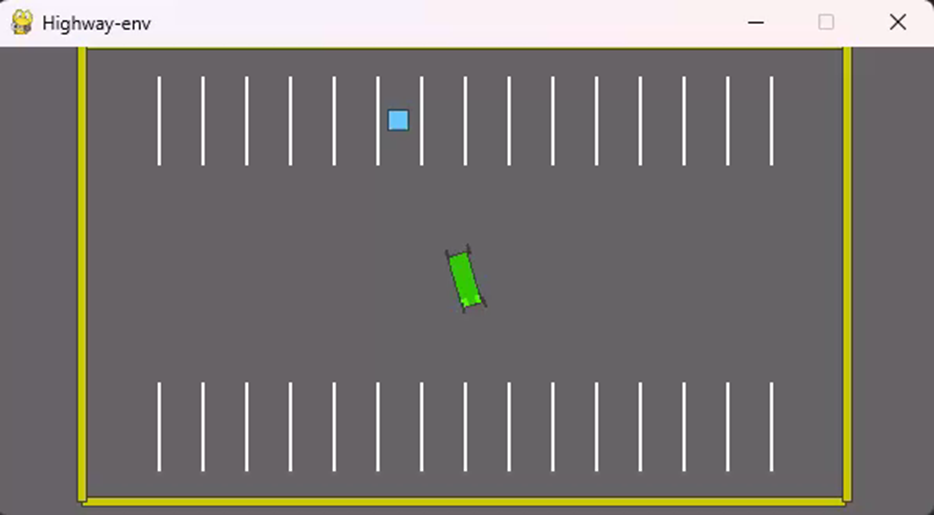
本来自己写了一个SAC模型用于测试parking环境(http://highway-env.farama.org/environments/parking/),该环境模拟自动停车过程,小车需要停到停车场随机的一个目标车位(见下视频)
无奈模型怎么也无法达到预期效果,经过多次测试发现,仅仅将DDPG修改为不确定性策略是可行的,但一旦加上最大熵(SAC的核心)模型就不不行了,然后使用stable-baselines3(https://github.com/DLR-RM/stable-baselines3/tree/master/stable_baselines3/sac)就可以,遂研究了一下两者代码的区别,发现,SB3默认会使用一个ent_coef的可学习参数,作为最大熵的系数,该参数可设置为固定值,以下分别为设置为固定值和可学习参数得到的效果:
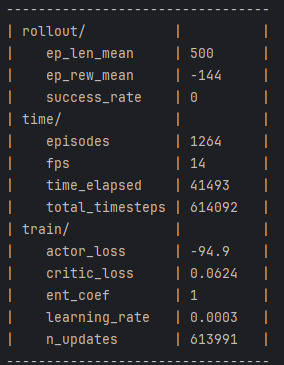
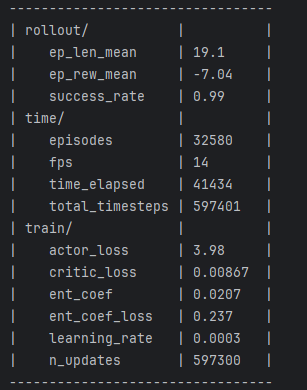
使用固定值为1的效果,见日志中的 train/ent_coef,从最终效果中可以看到,好像小车有那么一点点趋势会向目标点靠近,但不多
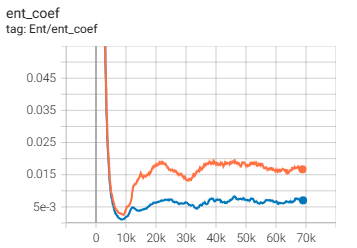
注意到 train/ent_coef 的值经过学习后变得很小(初始值为1),仅为0.02,从视频也能看到模型训练达到了预期的效果
随后我在我自己的SAC代码中也加入该可学习参数,发现确实也work了,该参数经过一段时间的学习也变得非常小:
分析
对于SAC来说,貌似有两个理论上很少提到但是实际上又不可或缺的东西
log_ent_coef 最大熵的温度控制
该参数原始代码大概长这样:
# 定义一个可学习参数
log_ent_coef = torch.log(torch.ones(1, device=device)).requires_grad_(True)
ent_coef_optimizer = torch.optim.Adam([log_ent_coef], lr=1e-3)
...
# 将上述参数作为 -log_prob 的系数,即最大熵的系数
ent_coef = torch.exp(log_ent_coef.detach())
target_Q = self.critic_target(next_states, act_next) - ent_coef * log_prob_next.detach().sum(dim=1).reshape([-1, 1])
...
# 参数学习
act, act_log_prob = actor(current_states)
ent_coef_loss = -(log_ent_coef * (act_log_prob - np.prod(env.action_space.shape)).detach()).mean()
ent_coef_loss.backward()
如何理解这个loss函数呢?以下是我由果推因的想法:
将loss单独拿出来看:
ent_coef_loss = -(log_ent_coef * (act_log_prob - np.prod(env.action_space.shape)).detach()).mean() # np.prod(env.action_space.shape)=2
需要先说明的是,act_log_prob 这个变量是当前policy在当前state下得到的动作的log probability,由于模型输出的是一个高斯分布,其均值和方差可能为任意数,所以高斯密度函数输出的值也可能为任意数,故而 log probability 也可能为任意值,有正有负。
DDPG训练时如何判断有效收敛
注:本文没有给出真正的答案,只是作为一个记录
有效收敛是我自己创造的词,例如在训练过程中,模型收敛到输出与输入无关的状态,或者其他意料外的状态则为无效收敛,反之为有效收敛
DDPG的基本思想是 先训练一个critic,然后使用该critic训练actor,接着再用该actor训练critic。。。不停迭代,和GAN类似
DDPG用到了一些trick,但我在实验中发现,对于某些任务,一些trick是无效的,为了验证哪些无效,我做了一些对比实验,本文目的不是记录这些实验,而是对比有效和无效的情况下,critic loss和actor loss的不同,我觉得这应该也能作为判断是否有效收敛的一个依据。
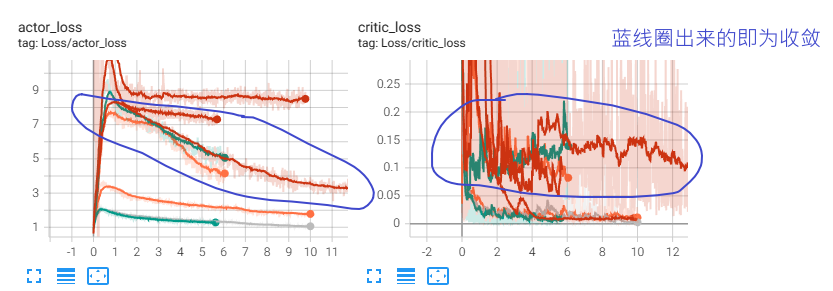
该实验可以通过critic loss明显看出有效收敛和无效收敛的区别:有效收敛的critic loss一直处于波动状态,并且不会收敛得很快,而出问题的那几个反而很快就收敛到0附近了
我想这应该是有一定道理的,因为critic和actor相互轮流训练,两者互相依赖,所以critic loss不应该收敛很快,因为actor一直在变。收敛很快很有可能出现 输出与输入无关 的情况,例如agent玩lol时,无论开始选择什么英雄,agent都会选择直接送塔,以避免被杀带来的损失。
DDPG中各trick效果对比
本实验仅仅是一个简单的实验,用于比较在 “Pendulum-v1”(gym提供的一个小游戏,用于训练RL模型)环境下,使用:
-
double net:critic和actor都拷贝一个副本,并延迟同步参数,在计算目标q值时使用改副本进行计算
-
每轮迭代次数:之前都是一局游戏结束就从历史数据中sample一批数据更新一次网络,而这里就是进行多次sample然后更新多次
-
replay buffer:将之前采样的数据都保持在一个队列中,训练时就从队列中随机采样数据
三者对模型训练性能的影响。注意:这个实验的结果并不能说明太多问题,不同的环境下,它们的作用肯定也不尽相同,我也仅仅是做一个记录而已。
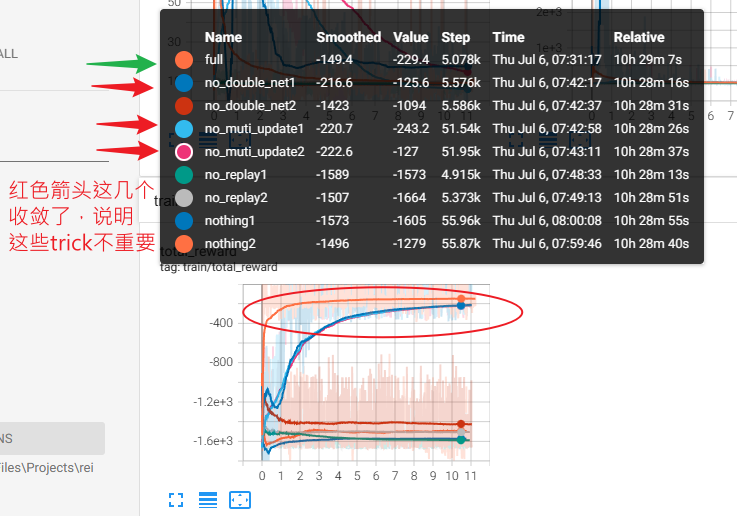
下图为各组实验在运行几个小时之后,在游戏中可以得到的reward
以full(所有trick都用上)作为对比,每个实验都做两组(上图中name后标有1,2),实验表明,在没有 “muti_update”(每一局游戏结束后,都对模型进行n轮训练,数据也都是历史数据中sample) 时,性能不会下降,只是比full收敛更慢,说明它不是很重要,只影响收敛速度,而不用 double net 时,一次可以达到理想水平,一次每练出来,即使是达到理想水平那一次,也可以看到其前面有一个不小的波动,也说明了 double net 可能对模型训练的稳定性起到了一定的作用,而没有 replay buffer 的两个实验和什么都没有的两个实验都gg了,可能说明了replay buffer的重要性。
Ornstein Uhlenbeck 噪声
直观理解
在DDPG(一种强化学习方法)采集数据过程中,会在actor输出的action上加上随机噪声以获得更好的探索性。
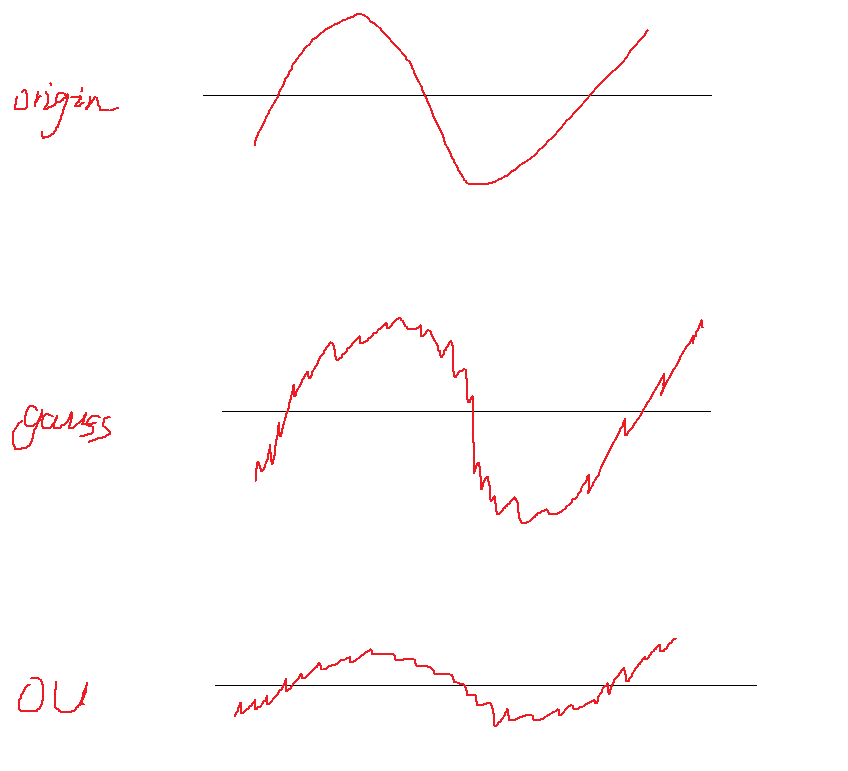
action是一个连续值,下图中的origin表示一个输出序列(一段时间内模型输出的action值)
最简单的加噪声方式就是直接在输出上加随机噪声,例如高斯噪声(第二行图像)
假如此时actor控制的是一个一辆汽车的方向盘,方向盘转动的角度是有限的,所以此时如果采用随机噪声的方式,则会有很多action被clip到最值,也就是浪费了很多探索的机会。
OU噪声的基本思路就是,先将原始值往其历史均值靠拢一点,然后再加噪声,这样一来,噪声被clip的几率就大大减小,同时,还能通过超参数控制将原始值向均值靠拢多少(上图第三行的图)
数学理解
OU噪声公式为:
事实上理解起来相当简单,将其换一种形式写出来就是:
\[ X_{new} - X_{old} = -\theta (X_{old} - \overline X) + βW\ ]
它分为两部分:\( \\theta (X\_{old} - \\overline X) \\) 表示当前输出X与历史均值的差值,前面加个负号表示如果大于均值就往回拉一点,反之亦然。\( βW \ ) 则表示一个随机噪声(例如高斯噪声)
这里的两个超参数 θ 和 β 分别用来控制 1)往均值方向拉多少。2)添加多大的噪声
Actor-Critic优缺点
译自:https://www.linkedin.com/advice/0/what-advantages-disadvantages-using-actor-critic
优点:
1. 通过将critic net输出的q value作为baseline,可以降低policy gradient算法带来的误差,使得使用较少数据就能够使模型收敛
解释:PG算法性能好坏很大部分取决于采样的数据,假如某游戏绝大部分都是正reward,则PG会无脑增大它采样到的action概率,即使有些action并非好的决策。一个解决办法是使得reward有正有负,且概率为0.5。即将采样得到的reward减去reward的期望,在qlearning中,这个期望就是critic net的输出。
2. 原始的PG必须等到一局游戏结束才能训练,而引入critic net之后,它就可以实时训练而无需等到游戏结束。
解释:原始PG需要计算整局游戏的得分才能训练,所以必须得等到游戏结束,而引入critic net后,因为它的作用就是预测该局游戏可能的得分,所以就不需要等游戏结束了
3. 对于不同的应用场景,可以使用不同的critic net来训练同一个policy。例如使用 状态价值函数 或 动作价值函数作为critic net等
缺点:
1. 可以想象,如果critic net没有收敛,那用它训练出的policy肯定是有问题的,这大大增加了模型的训练成本和风险
2. 使用两个网络使得算法实现更为复杂
policy gradient处理连续动作空间
policy gradient可以直接输出action的概率来进行离散动作的选择,而对于连续动作空间,则需要直接输出动作的值,需要想办法将其转换为概率,方法就是输出一个action的分布(例如输出正态分布,就让模型输出 均值 和 方差 两个值即可),然后从该分布中采样一个action,进而计算该action在该分布中的概率,使用模型提高这个概率即可。
以下为连续动作空间的代码示例:
mean, std = actor(states)
action_distribution = torch.distributions.normal.Normal(mean, std)
action = action_distribution.sample() # 采样action
prob = action_distribution.log_prob(action) # 获取该action在输出分布中的概率,后面就是和离散型的一样了
_, reward, _, _, _env.step(action)
loss = reward * prob
loss.backward()
...
作为对比,以下为离散动作空间的代码:
action_probs = actor(states)
action = torch.distributions.Categorical(action_probs).sample() # 采样action
_, reward, _, _, _env.step(action)
loss = reward * torch.log(action_probs)
loss.backward()
...
SAC、TD3、DDPG
本文不讲理论上的东西,只说实现上的不同。
事实上,如果单从实现来看,SAC和DDPG的差别不大。从 stable-baselines3 看,区别仅仅在于,SAC在训练critic和actor时,多在reward上加了一个熵值,而这也正是SAC的特性来源。
关于什么是熵,可以参见 https://blog.woyou.cool/posts/100/。简单来说,它就是一个值,与事件发生的概率呈负相关关系。因为在reward上加了这个值,也就是说,action发生的概率越小,这个值越大,额外奖励就越多,也就能达到鼓励模型进行探索。当然不仅仅是鼓励探索,本质上还有很多其他的作用,但这里简单先这样认为就够了。
SAC的训练仍然是同DDPG,在每轮训练中,先优化critic的参数,然后基于优化后的critic来优化actor的参数,区别仅仅是reward多了一项。
TD3是DDPG的改进,就像qlearning中引入dqn一样,使用两个critic网络,但是这两个网络独立更新,每次选择q值的时候就从两个网络中选择较小的那个,防止q值被高估。再者,TD3不会像DDPG那样每次迭代都同时更新critic和actor网络,而是critic每次都更新,但隔一段时间才更新actor。另一点就是引入了噪声增加鲁棒性
一些参考:
openAI关于强化学习的教程:https://spinningup.openai.com
openAI给出的各种强化学习基本实现,第三方优化版本 Stable Baselines3:https://github.com/DLR-RM/stable-baselines3/tree/master
Soft Actor-Critic Demystified,这篇文章给出了早期SAC的迭代公式并配有相应pytorch实现,早期的SAC有 Value network、Q network、Policy network 三个网络需要更新,而现在基本只更新 value 和 policy 两个网络:https://towardsdatascience.com/soft-actor-critic-demystified-b8427df61665,这个是他的代码:https://github.com/vaishak2future/sac/blob/master/sac.ipynb
深度解读Soft Actor-Critic 算法:https://zhuanlan.zhihu.com/p/70360272
PPO:on policy OR off policy?
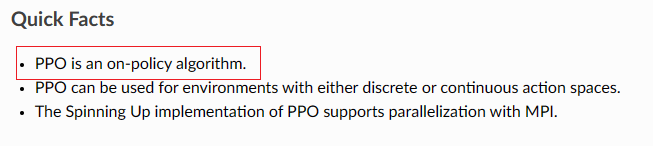
之前看李宏毅关于强化学习视频的时候,他说PPO是 off policy 的方法,但是刚看openai spinningup的时候,里面又明确写明它是一种on policy的方法。
如何区分
我个人觉得,一个非常简单的区分方法为:如果与环境交互的策略与目标策略相关,则是on policy的,否则是off policy的。
注意:我这里说的是“相关”,而严格定义来说应该是“相同”,为什么要这么区分,这就和本文题目有关了。
举两个典型的例子进行说明:
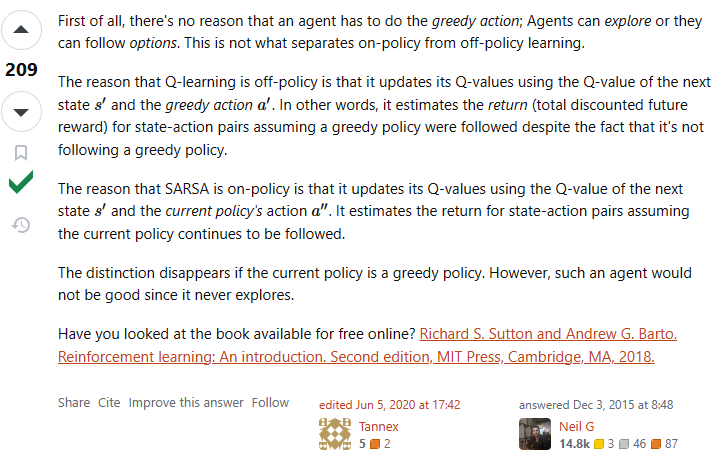
Q-learning:典型的off-policy策略。Qlearning在数据收集(与环境交互)过程中,可以采用任意策略,收集到的数据可以长久保存下来用于qtable或qnet的训练。这是因为训练得到的qtable或qnet本身就与模型无关,你可以使用它训练任意actor网络
SARSA:典型的on-policy策略。它和Qlearning唯一的区别在于,qlearning是直接找到\( S\_{t+1}\\)中最大的reward,而SARSA找到当前策略在\(S_{t+1}\ )时的能够获得的reward。显然,一个和目标策略无关,一个有关。
两者Q值的更新公式:
注:2式中,\( a\_{t+1} \\)表示的是当前策略在\( S_{t+1} \ )环境下所选择的action
还看到另一种解释,我觉得更精简得说明了这个问题,但思想差不多:
PPO?
从上面说的角度来看,PPO确实应该归属于on policy策略。因为它收集数据所使用的policy与目标策略是相关的,这里的相关体现在收集数据所使用策略的参数必须每过一段时间与目标策略参数进行同步,它们不能相差太大。
但是如果从严格定义上来讲,虽然两个策略必须保持相似,但本质上还是两个策略,从这方面来说,它确实也是off policy的
正梯度仍然使得policy的probability增大
现象
使用policy gradient算法写了一个小模型,训练过程中发现模型很快会收敛到一个非常糟糕的结果,理论上不应该呀,因为按照policy gradient算法原理来说,对于某个action,如果你给了负的reward,那么模型会减小该action出现的概率,但我的实验表明,模型不仅没减小该action的概率,甚至还会增加它的概率,最终它的概率甚至会等于1。理论上,即使这个不好的action概率为1了,但是reward是负的,每次迭代应该还是会降低其概率,但我这个实验发现并没有,反而会继续降低另外一个好的action的概率——即使它已经无限逼近0了。
排查
首先我想,既然坏的action概率在增加,有没有可能是因为reward是正数(本来应该给负数),但是经过简单的排查后发现,该action的reward就是负数。
然后考虑到,policy gradient 对采样的样本action会无脑增大其发生概率(前提是该action的reward是正的),然而采样所使用的概率也是这个概率,那么就可能形成一个恶行循环:梯度上升导致概率增大->概率增大导致其更容易被采样->采样后概率继续增大…。但经过计算发现,即使它的概率会恶性增大,但如果采样的足够多,总是会采样到其他reward更大的action上,那么它的概率还是会减小很多。另一点就是经过排查,发现这个action的reward确实是负的,应该不会出现这个情况。
第三个想法是,因为这是一个神经网络,本质上就是一个函数,假如这个函数有图像的话,现将其简化想象成一个二维的曲线,那么上面的问题就类比于:如果我采样到上面某个点,经过计算发现下一次迭代后,这个点的位置应该下降(本质上是函数发生了变化,原本的函数更新为另一个新的函数),但是实验却发现下一次迭代后它还上升了。一个很直接的想法就是,有没有可能,如果单独更新这一个点时,它确实会下降,但实际上,我同时更新了多个点,在更新其他点时,更新的参数影响了这个点的值,那么它就有可能不降反升。理论上,这也确实是非常有可能的,但它发生的概率应该要远小于50%,否则模型只会越训练越差。但上述实验发现,好像这个值又接近50%,这就让人匪夷所思了。而且,理论上,就算出现这种问题,在迭代次数足够多后,这种情况应该越来越少。所以这个假设也被排除。
实验到此已经很晚了,我仍然没想通什么原因。于是我想会不会就算训练的时间不够导致的,于是我同时运行好几个相同的模型,其中只有部分有修改,例如有些使用 discount reward,有些使用 total reward,有些则更换优化器等,跑一个晚上看看结果。
如何使用梯度判断模型中间量的更新方向?
在pytorch中,只有叶子节点的变量(学习量)才可以直接获取梯度,但在上述问题中,我发现模型输出的某个概率增大了,我怀疑这里的梯度有问题,那么我想查看这个输出概率的梯度怎么办?很明显直接看是看不了的,因为它只是一个中间量,虽然会计算它的梯度,但并不会在backward后保存下来,因为并不需要真正更新它。
pytorch提供了 register_hook() 函数来获取或修改这些中间量的梯度:
output = model(input)
...
# 如果同一个变量注册了多个 hook,则会顺序执行它们。
output.register_hook(lambda grad: print(grad)) # 读取梯度
output.register_hook(lambda grad: grad * 2) # 也可以直接修改梯度
...
loss = loss_model(output)
loss.backward() # hook中的函数会在这里计算完梯度后执行
...
通过这种方法,你就可以知道下一次迭代时是会增加这个输出还是会减少这个输出了。由于迭代后的值等于原值减去梯度,如果梯度是正数,则会减小,反之会增加。下面是一个register_hook()使用方法的例子:
a = torch.tensor(2., requires_grad=True)
b = 5 * a
c = b * b
b.register_hook(lambda g: print(f'b grad: {g}')) # b grad: 20.0,因为用c对b求偏导为 2b, 而b又等于 5*2,所以b的梯度为 2 * 5 * 2
c.backward()
一个具体的例子:
Policy gradient中为什么必须给概率取log?
注意:这篇文章没有解释原因,只是探索了一个相似方法
一般认为是可以用来简化计算的,log可以将原本的累乘转换为累加,例如 a*b*c 总体加上一个log就可以转换为 loga+logb+logc,当然,能总体加log是因为log保留的原来函数的单调方向,转成加法还有个好处就是一定程度上可以防止梯度消失或爆炸,因为连乘很容易为0或无穷
使用最朴素的policy gradient写了一个玩平衡杆的策略模型,发现如果使用SGD会出现一些问题
# 以下代码是有问题的
...
action_probabilities = model(current_env)
...
choose_action_prob = action_probabilities[choose_action]
...
loss = -reward * choose_action_prob
loss.backward()
...
问题出现在直接使用 choose_action_prob 用作梯度上升。
其实直观上感觉应该就是这样的:一局游戏的得分的期望等于这局的total reward乘以这局游戏中各个过程的出现概率。目标就是最大化这个期望,如果使用现有的梯度下降框架,则直接在前面乘以一个负号即可。感觉应该就是这样的,实验结果表明这样模型很有可能不会收敛,模型不会选择最优策略。
我猜测问题可能出现在负号上,理论上这个loss可以无限小,也就是它可能是无解的,但可以通过修改代码使得模型可以趋近于一个值(注:问题原因并不一定是这个,我猜的,但这个解决方法确实可以解决这个问题)
解决方法是让 choose_action_prob = -1/choose_action_prob,因为我们的目的是使得上面的loss更小,也就是使得这里的choose_action_prob更大,前面加上一个负号就可以让它和loss前面的负号抵消,然后让它做除数,即不影响它原本的单调性。
我实验了一下,这种方法确实可行,但更常用的方法是取log
# 方法一
choose_action_prob = 1/choose_action_prob
loss = reward * choose_action_prob
# 方法二,注意后面加一个很小的数防止为0
choose_action_prob = torch.log(choose_action_prob + 1e-8)
loss = -reward * choose_action_prob
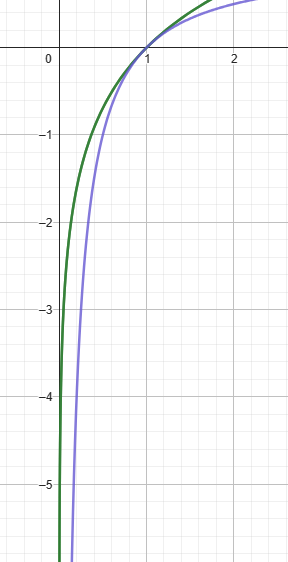
这样一来,loss应该是越趋近于0越好。不过实验结果表明,方法二的效果远远好于方法一,甚至于 -1/x+1 也比上面的1/x要好得多,why?
这是 log_e(x) 和 -1/x+1 的曲线
以下为完整代码:
import itertools
import threading
import gymnasium
import numpy as np
import torch
from loguru import logger
from torch.utils.tensorboard import SummaryWriter
board = SummaryWriter('./logs/division_factor_random')
torch.random.manual_seed(1)
np.random.seed(0)
def visualize_train(policy: torch.nn.Module):
with torch.no_grad():
test_env = gymnasium.make("CartPole-v1", render_mode='human')
for i in itertools.count():
total_reward = 0
obs, _ = test_env.reset(seed=0)
while True:
action = torch.argmax(policy(torch.FloatTensor(obs)))
obs, reward, terminated, _, info = test_env.step(action.item())
total_reward += reward
if terminated:
board.add_scalar("test/reward", total_reward, i)
logger.info(f"total reward: {total_reward}")
break
test_env.close()
class Actor(torch.nn.Module):
def __init__(self):
super().__init__()
self.dnn = torch.nn.Sequential(
torch.nn.Linear(in_features=4, out_features=20),
torch.nn.ReLU(),
torch.nn.Linear(in_features=20, out_features=2),
torch.nn.Softmax(dim=0)
)
def forward(self, x):
return self.dnn(x)
actor = Actor()
threading.Thread(target=visualize_train, args=(actor,)).start()
optimizer = torch.optim.Adam(params=actor.parameters())
env = gymnasium.make("CartPole-v1", render_mode=None)
for game_count in itertools.count():
obs, _ = env.reset(seed=0)
acts = []
rewards = []
for s in itertools.count():
action_probs = actor(torch.tensor(obs, dtype=torch.float))
action = torch.distributions.Categorical(action_probs).sample().item()
# if np.random.random() < 0.1: action = np.random.randint(0, 2)
obs, reward, terminated, _, info = env.step(action)
acts.append(1 / action_probs[action])
rewards.append(reward)
if terminated:
# loss with discount factor=0.99
loss = sum([a * weighted_r for a, weighted_r in zip(acts, [sum([r * 0.99 ** j for j, r in enumerate(rewards[i:])]) for i in range(len(rewards))])])
# loss = (sum(rewards) * sum(acts))
optimizer.zero_grad()
loss.backward()
optimizer.step()
break
env.close()
深度强化学习简介
这是一篇深度强化学习视频的笔记 https://www.bilibili.com/video/BV1XP4y1d7Bk
什么是强化学习
强化学习方法分为三类:Policy-based(训练一个actor,例如 policy gradient)、Value-based(训练一个critic,例如 Q-learning)、Actor-Critic
所谓的actor就是一个agent,即决策者,它能根据一个输入状态,输出一个行为。例如输入一帧游戏画面,它输出前进还是后退等,然后系统根据游戏结果给出相应奖励
所谓critic就是一个预言家。它用来预测某个人执行某种行为的预期结果
某人(actor)问预言家:我现在破产了(当前状态),如果我去抢银行或者去打工(可以采取的动作),我会得到什么后果?预言家说:如果你去抢银行,你会被抓住,后半生就在监狱度过,如果去打工,由于你的人品不错,你会遇到一个贵人,他会让你飞黄腾达(对这个人采取某个行为的预言)。
事实上,上面问预言家(critic)的过程就是Actor-Critic,actor不会真的去抢银行或者打工,他只是提出这个做法,让critic去评价,然后他得到这些评价内容后来审视自己,比如说他知道打工会遇到贵人是因为自己人品好,他就会让自己人品更好,而预言家看到了这个人的改变后又会给出新的预言,两者不断更新
关系梳理
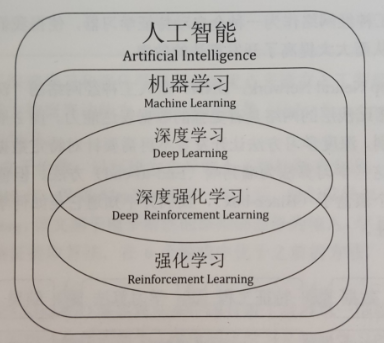
下面的图来源于《深度强化学习》一书,我觉得这些图对学习强化学习的路径规划有很强的指导意义
强化学习在人工智能领域的位置
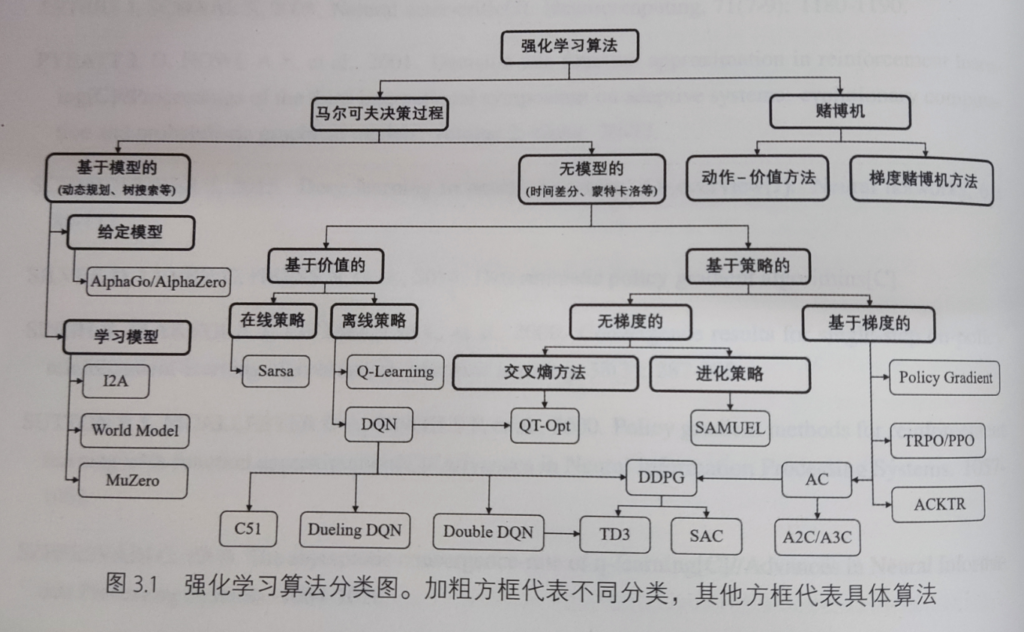
强化学习算法分类:
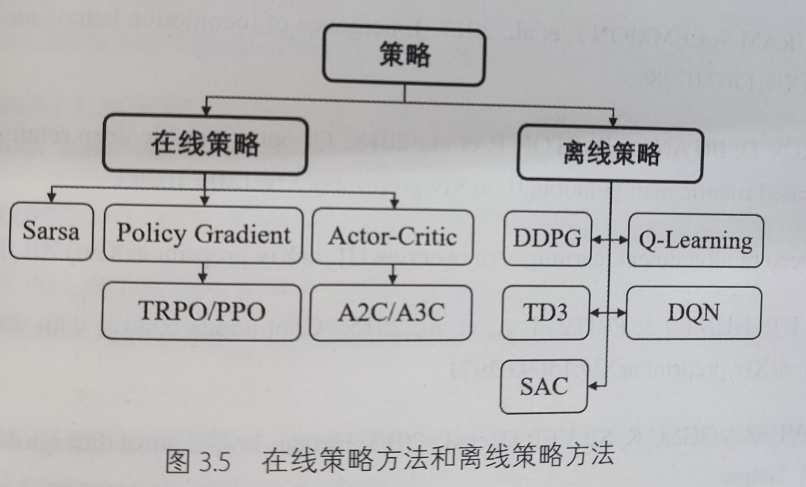
在线策略和离线策略分类
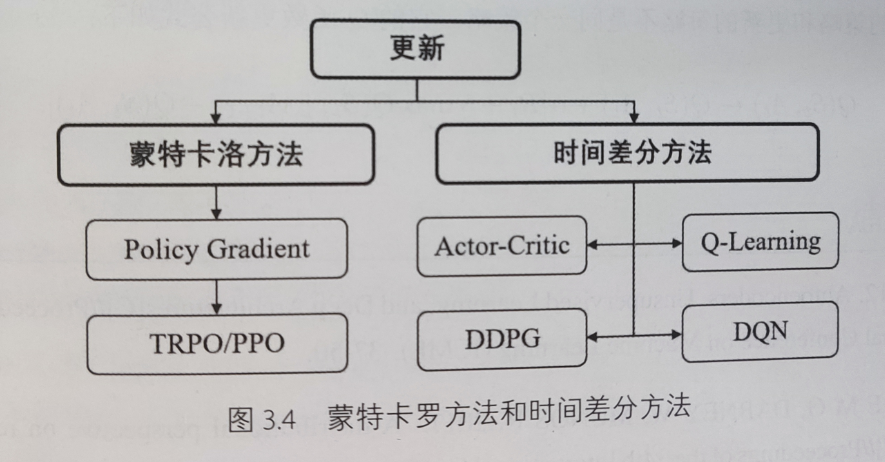
蒙特卡罗法(MC)和时序差分法(TD)分类
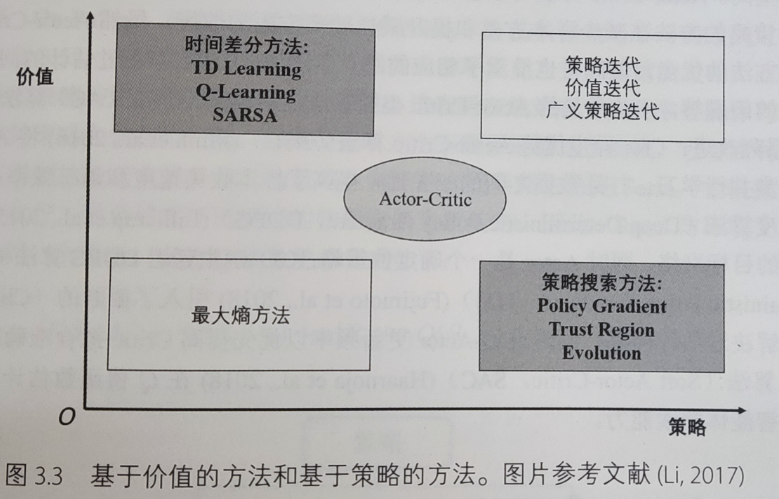
value-based 和 policy-based 方法分类
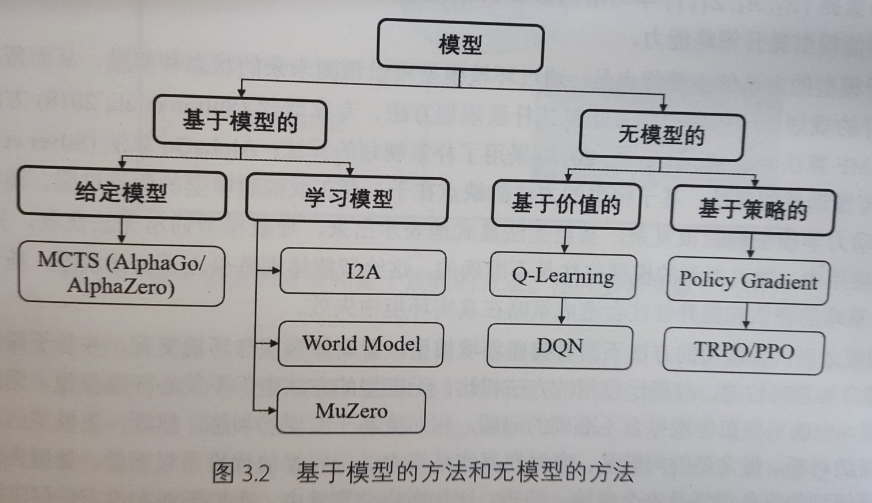
基于模型的方法和无模型的方法分类(不是深度学习模型,是数学模型)
policy gradient
每一局游戏都是由 状态-动作-奖励-状态-动作-奖励。。。不断循环进行的
\[ trajectory τ = {S_1, a_1, r_1, S_2, a_2, r_2…, S_T, a_T, r_T} \ ]
所以一个trajectory发生的可能性为:
\[ p_θ(τ) = p(S_1)p_θ(a_1|S_1) p(S_2|S1, a_1)p_θ(a_2|S_2)p(S_3|S_2, a_2)… = p(S_1)\prod_{t=1}^Tp_θ(a_t|S_t)p(S_{t+1}|S_t, a_t) \ ]
对于任意一个trajectory来说,它的total reward为:
\[ R(τ) = \sum_{t=1}^Tr_t \ ]
那么对所有trajectory来说,它的reward期望就是每个trajectory发生的概率乘以其total reward:
\[ \overline{R}_θ = \sum_τp_θ(τ)R(τ) =E_{τ\sim p_θ(τ)}