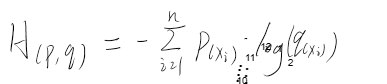深度学习

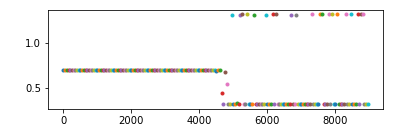
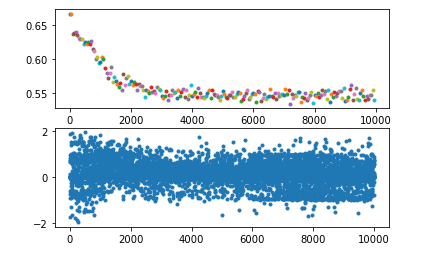
loss总是收敛到0.69左右

这种情况一般是在使用了交叉熵的二分类问题上容易出现，同样的，也可能出现loss收敛到1.0986、1.386等等，其实他们就是log(1/2)、log(1/3)、log(1/4)。。。

问题概述

根本原因：交叉熵

若q=0.5则对于01分布来说，H=log(0.5)=0.69，同理对于n分类问题来说，loss可能会收敛到log(1/n)，这都是因为各个类别拟合概率相近导致的，再看看为什么会导致各类别拟合概率相似

常见原因之一：Sigmoid

使用交叉熵之前通常会使用sigmoid作为激活函数，sigmoid公式及图像为：

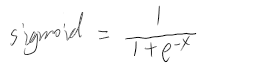
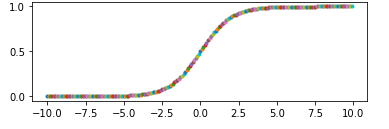
由此可知，有两种情况会使得sigmoid的输出都是相近的
1. 自变量x都是相近的，导致函数值也相近
2. 当自变量x大于或小于某个数之后（例如5和-5），其值基本就等于1或-1。那么如果上层神经元的输出都是一个较大或较小的数，则经过sigmoid之后得到数组元素就都是1或-1，则针对每个分类的概率就是相同的，这样的数据得到的交叉熵就是log(0.5)或者log(1/3)或者log(1/4)…
对于第一种情况，我们看看为什么自变量x会都相近。一般来说，线性函数的结果输入到sigmoid中，其公式为：wX=Y
由此可知，若要使得y中的元素相同，又有两种方式：
1. w中每一行都相同或相近
2. X趋近于0，则此时Y也会都趋近于0
再分析逐个分析
出现第一种情况一般来说可能是权重的初始值设置不合理，例如使用pytorch中的fill_函数使得所有的权重都相同，且后续训练也没有有效地更新权重导致的（为什么没更新权重后面会说），则可以选择一些更随机的初始化方法。
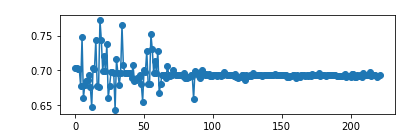
为什么权重没有更新：可能是学习率设置的过小或初始权重过大或情况二，一般来说，如果是学习率设置过小或初始权重过大，则在足够多的迭代次数之后，loss就会恢复正常

出现第二种情况则是数据源的问题（若全连接前还有其他层，则其他层的输出就已经很小了），此时可以通过normalize的方法对batch的数据进行处理或放大之后再输送到全连接层
对于第二种情况，较好的做法是在将数据送到sigmoid之前先进行normalize

以上只是两种特殊情况，下面将列举我目前能想到的五种情况

出现问题原因及解决方法

当输入与输出确实不相关时

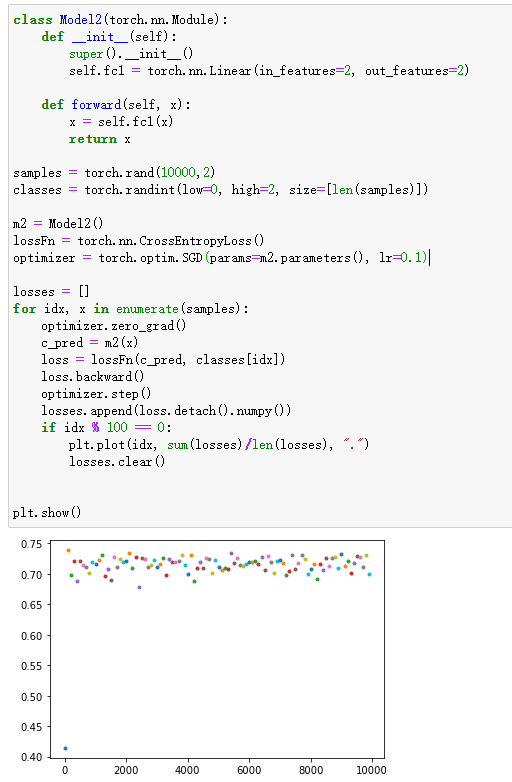
解释：这个很好理解，因为你的数据本身就不能拟合，所以不管是让人做分类还是让机器做分类都只能得到50%的正确率

解决办法：数据源上找原因

当模型初始权重相同且较大，且学习率较小时

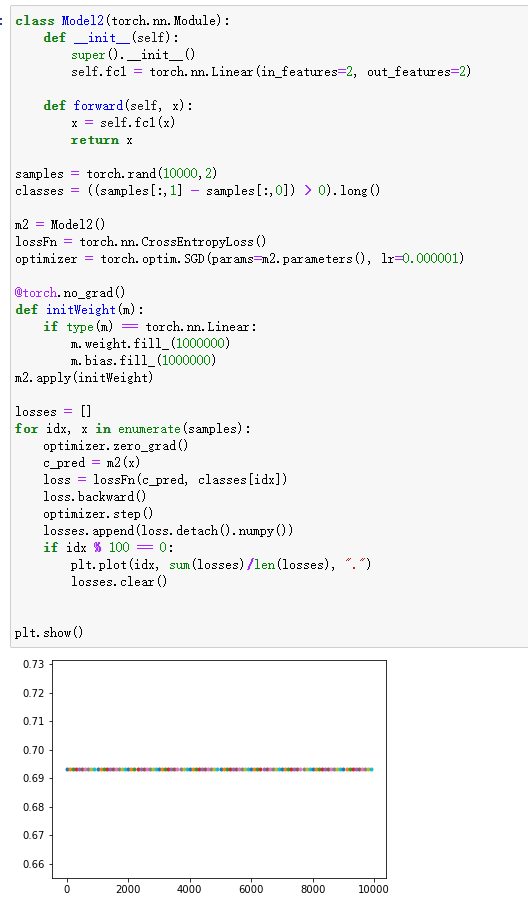
解释：权重相同则意味着模型预测每个分类的概率输出是一样的，学习率较小意味着权重更新幅度太小，导致即使经过了长时间的训练权重依然几乎相同——同初始值一样。

解决办法：理论上，出现这种情况，只要迭代的次数足够多，模型还是可以收敛的。也可以使用pytorch的norm_方法初始化权重，并增大学习率

当模型的输入本身就很小，或者模型初始化权重很小时

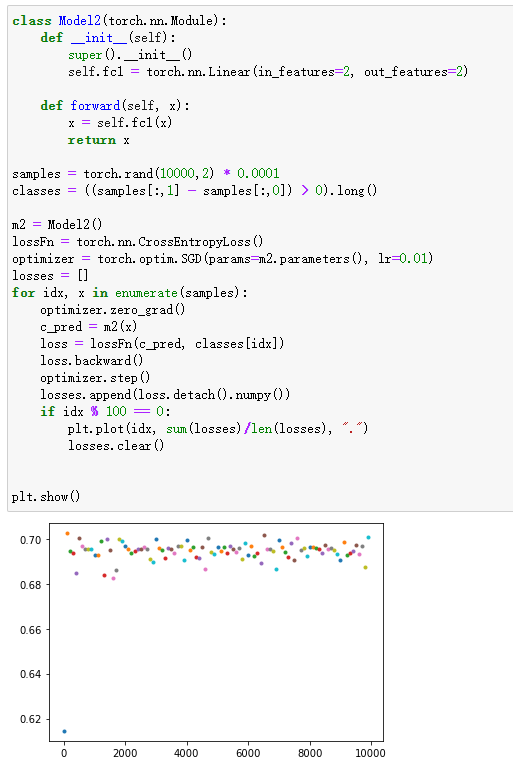
解释：两个原因，1. 由于预测输入是通过线性函数 w*x + b=y 得出的，如果此时x或w趋近于0，则得出的y也都是趋近于0或偏置b的，最终导致模型对各个类的概率相同。2. 同下方的将输入整体放大的情况

解决办法：对输入做normalization处理，合理初始化权重，比如使用N(0,0.001)分布初始化权重

特征不明显，导致长时间训练不拟合

解释：emmmm

解决办法：做一些特征工程，多迭代迭代应该也能跑出来，增加模型复杂度或许也有用

使用sigmoid或tanh这类函数时，将输入特征整体放大后使得收敛更困难

解释：从pytorch文档中可以看出，lstm使用了很多sigmoid和tanh激活函数

这两个函数都有一个特征，就是他们的导数在大于或小于某个范围时几乎等于0，这就导致backward时梯度越来越小，进而导致权重无法更新或极慢，如下图

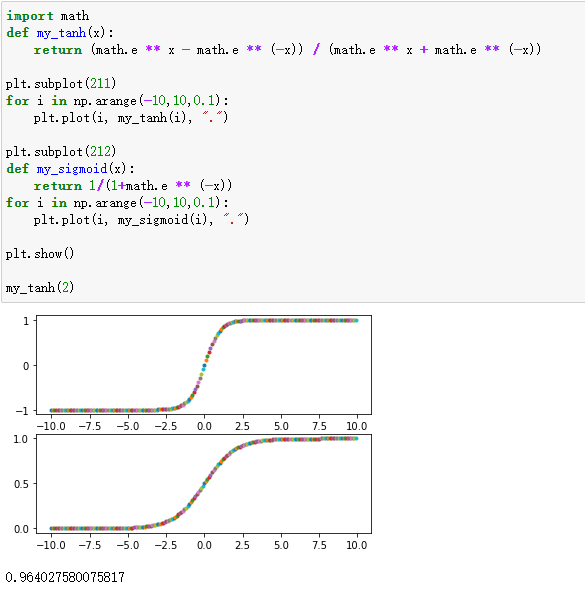
所以如果输入lstm的值都比较大或比较小，从官网给出的公式不难看出，其输出就容易只在0、1、-1三个数附近徘徊（如下图中的第二个图）

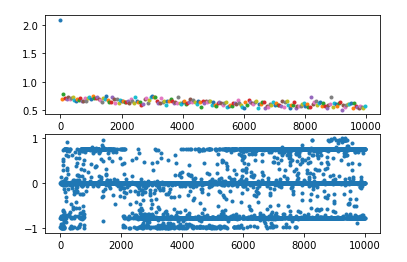
解决办法：解决办法很多，这里写三种

想要解决这个问题就得在lstm的输入端做一些处理，比如，我这里使用sin函数将值域固定在某个范围内，起到了一定的效果

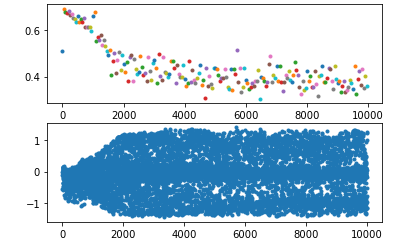
或者，直接使用pytorch提供的layerNorm

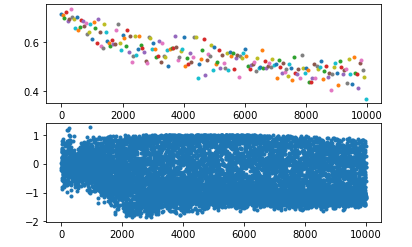
或者，当我不进行norm只使用batch输入的时候，批量化处理会排除个别元素干扰，对整个batch求均值能提高收敛速度减小训练时间

交叉熵

信息量

用于描述事件包含的信息。一件事发生的概率越小，则其信息量越大。如

事件A：“Hunt当选了国家杰出青年称号”

事件B：“Hunt当选了学生会主席”

两个事件都有可能发生，但他们所蕴含的信息是有差别的，比如，若要发生事件A，则Hunt至少满足四个条件：Hunt年龄小于四十五岁、Hunt具有博士学位、Hunt有较好的科研成果、Hunt曾在高校或科研所工作。但若只是事件B发生了，我们能知道的仅仅是：Hunt是一名学生。显然，事件A的信息量大于事件B，且事件A发生的概率P(A)要小于事件B发生的概率P(B)

则某个事件发生的概率越小，其信息量越大。

信息量与发生概率负相关，且当某件事x的发生概率为1时，其信息量应该是0，若发生概率无线小，则其信息量应该无限大，log函数能较好匹配这个条件，由此可以得出信息量的公式：

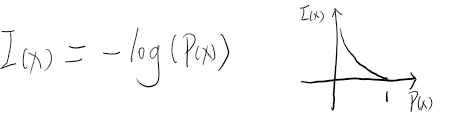
熵

一个系统是一系列事件的集合，比如我们生活中无时无刻不在发生着各种各样的事件。熵则表示这整个系统中所有可能发生事件的信息量期望。若一个系统所有可能出现的事件总和为n，每个事件xi发生的概率为P(xi)，则熵的公式为：

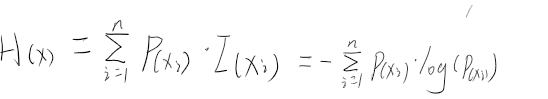
若将抛掷一枚硬币单独看成一个系统，则该系统由两个事件组成：抛正面（概率为p）和抛反面（概率为 1-p），则上式可写成：

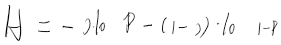
相对熵（KL散度）

假设现在我让你去猜某个系统中所有事件发生的概率，对于有n的事件的系统，第i个事件真实发生的概率为 P(xi)，而你的猜测是Q(xi)，如何衡量你猜的是否准确呢？最简单的办法就是使用Q(xi) - P(xi)，其绝对值越小，则说明猜的越准。对于整个系统来说，我可以将简单的概率猜测差值转换为系统熵的差值，则公式为：

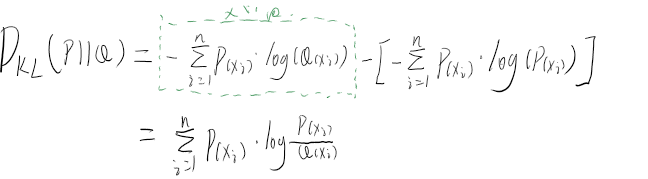
交叉熵

相对熵描述的是对同一个随机变量两种不同分布的差异大小，在机器学习中，我们需要制定一个损失函数并设法将其值减小以使得机器学习的拟合度更高，则相对熵较好匹配了这个要求。相对熵越小，则说明我们猜测的概率Q越接近真实概率P。

从相对熵的公式可以看出，若要最小化相对熵，由于真实熵是一个常数（设为M），根据吉布斯不等式可知，KL散度一定是大于0的，所以只用减小猜测的熵值即可，则将真实熵移到等号左侧。剩下的就是我们猜测的Q所产生的熵又被称作交叉熵，这和直接使用相对熵是等价的

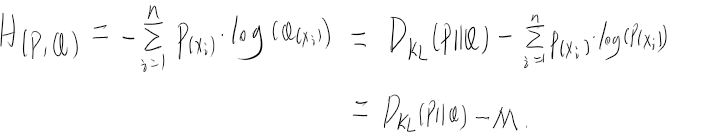
吉布斯不等式

来源：https://blog.csdn.net/m0_37805255/article/details/95587461