Fari

Opencv

opencv不同环境下output不一致的一种场景

现象

opencv在c++和python中得到的结果不一致，即使是相同的语言相同的环境也可能得到不同的结果。

在做一个视觉项目时，其中有使用opencv，开发过程中我会先使用python写出基本的代码进行测试，可行的话再用c++（qt）复写一遍，本机测试完成后上传到服务器实机测试，一开始开发过程还算正常，后面就发现，服务器上有些图片识别的有问题，遂将有问题的图片都过程保存成 xxx.jpg，然后拉到本地看看啥问题，结果本地识别起来又没问题，甚至于有的时候，使用python处理后得到的中间结果再用c++继续处理就会出现和只用python处理的结果不一样。

这种情况并不普遍，几千张图片可能出现几个异常的情况。拉下来后本地又识别得没问题。

排查

一开始以为是缓存的原因，但是仔细重构代码后排除了这种可能

然后以为是并发的原因，因为之前也出现过一次使用qt出现的并发问题，多线程下一个野指针出现的问题，也是小概率出现，也是折腾了很久才解决。

反正就是搞了很久，还是无法百分百确定是不是并发造成的，于是想想是不是其他原因

甚至于我将每张出问题的图片的每个中间处理过程都保存下来和本地进行对比，输入一样（目视）但结果就是会出现不一致

最后，我将每张图片都保存后让程序进行重放（按原来顺序重新检测），经过对比发现，不是随机出现的，遂确定不是并发导致的，于是我将出问题的图片单独进行检测，奇迹出现了，不管是本机还是服务器，检测结果都一致了，我又试了多次，确实是一致的。

我的代码中，出问题的地方主要是霍夫圆检测上（HoughCircles），该函数基于Canny算子做边缘检测，然后我发现之前出问题的图片，虽然输入的图像目视是一样的，但Canny处理后的结果会出现些许不同。虽然不同的地方还是比较少，但我觉得霍夫圆检测对参数还是比较敏感的。

然后我突然想到，之前不一致的情况都经过了一次中间过程的存储，然后再进行读取的，那问题一定是出现在存储格式上。

解决

问题就出现在jpg这种图片格式上，其实从一开始我就有想到这个东西，因为我一直对傅里叶变换比较感兴趣，而jpg就是用该原理实现的，但不知道怎么的，后面忘了这茬了。将图片以位图的形式保存就好了。

// 原来的
cv::imwrite("img", "xxx.jpg")
// 现在的
cv::imwrite("img", "xxx.bmp")

后记

有一说一，c++/qt 好像做什么都比较麻烦，还不好debug，用惯了jetbrain的ide再用qtcreator感觉就像回到了上个世纪。

Windows下编译并测试OpenCV

注1：以下若不做说明默认将opencv下载编译到我本机 C:\Users\HuntZou\Downloads\ 目录下，您需根据您自己的情况做一些替换。

注2：以下若不做说明则都是我自己试过的方法

编译

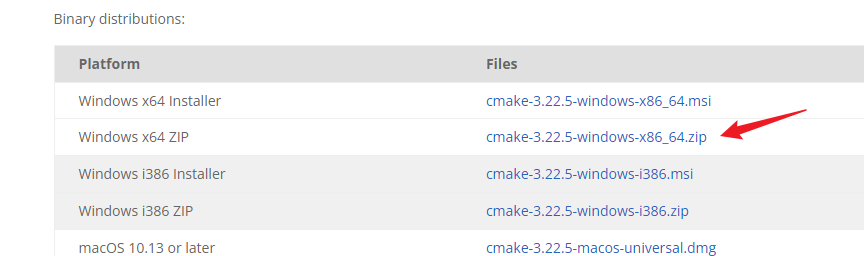
1. 下载cmake

https://cmake.org/download/

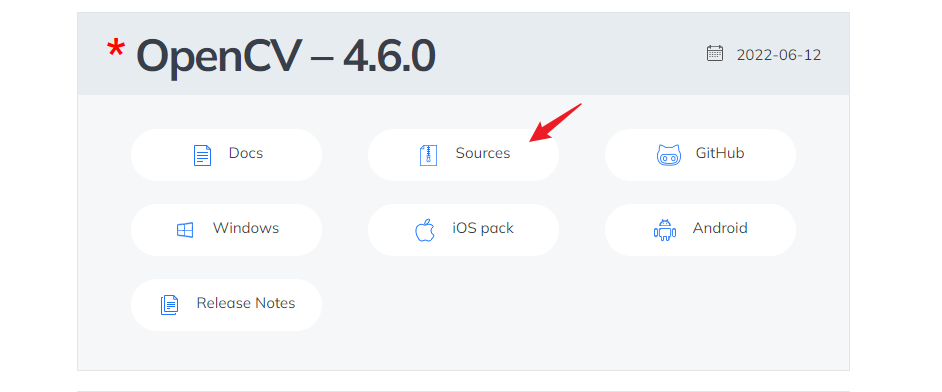
2. 下载opencv源码

https://opencv.org/releases/

3. 解压缩opencv源码并进入到解压后的目录

4. 在解压后的目录创建一个build目录，用于存放cmake的输出文件

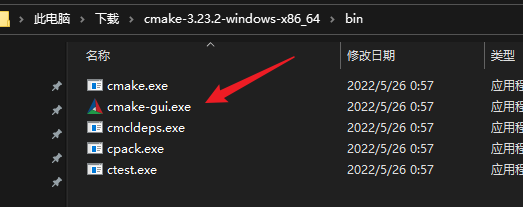
注：这是为了后面在命令行中使用cmake，你也可以直接使用cmake的gui

5. 在build目录中打开cmd，并使用下载好的cmake创建makefile

这一步需要下载一些东西，由于东西在外网，导致在这里卡半天，最终会报错

解决办法：

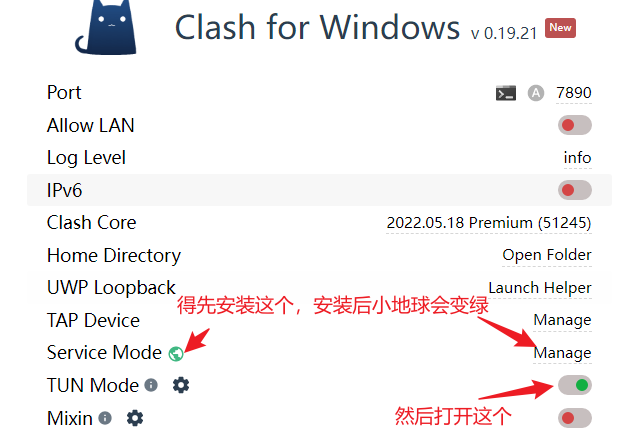
5.1 简单方法（使用代理）：如果电脑上装了clash代理软件的话，直接开启clash的tun模式即可，我自己实验一次就成功了。

貌似windows命令行默认不走代理，clash开启该选项后会虚拟出一块网卡，所有流量都会经过该网卡，这样即使不走代理的软件也会被迫走代理。

貌似也可以直接设置命令行走代理，不过我没试 https://blog.csdn.net/u014723479/article/details/103698296

5.2 复杂方法（cmake期间不用下载）：

5.2.1. 自己在下载好该文件

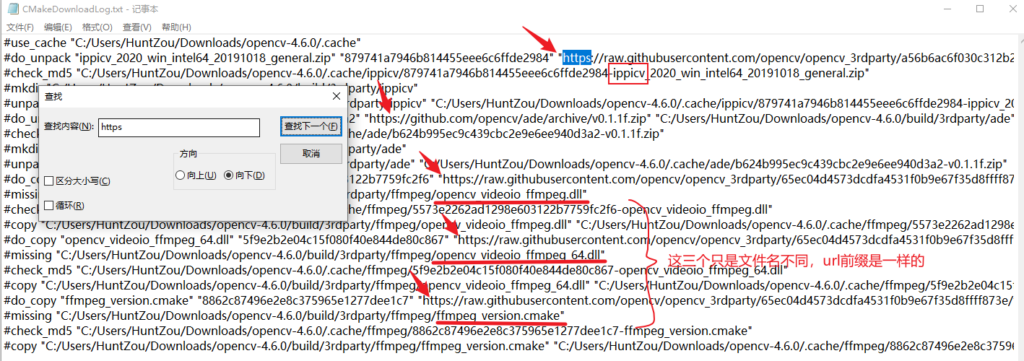
停止cmake，然后找到build目录下的 CMakeDownloadLog.txt 文件，在里面搜索关键字 ”https“ 可以找到文件的下载链接。

注：图示内容为可以正常下载情况下的截图，您该文件内容应该没这么完整，但也能找到一些url链接。

需要下载的文件一共有四个，共分为两类：

ffmpeg：opencv_videoio_ffmpeg.dll、opencv_videoio_ffmpeg_64.dll、ffmpeg_version.cmake

ippicv：ippicv_2020_win_intel64_20191018_general.zip

ippicv的链接直接下载即可

ffmpeg需要下载三个文件，但它们的url前缀都是一样的，将上述三个文件名替换一下下载即可

5.2.2. 将下载好的 ffmpeg 三个文件 放到 /3rdparty/ffmpeg/ 目录下

ippicv_2020_win_intel64_20191018_general.zip 放到 /3rdparty/ippicv/ 目录下

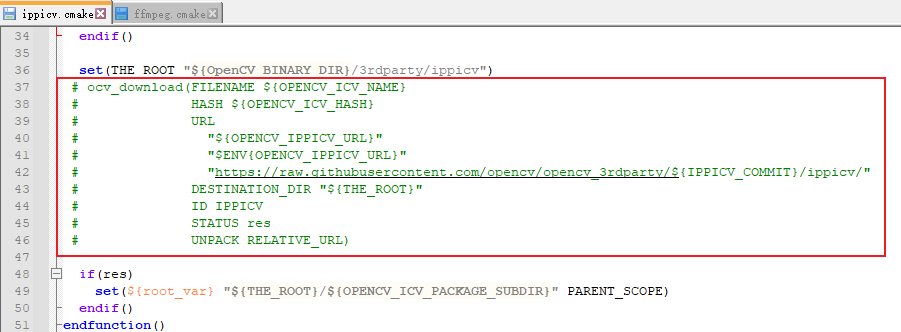
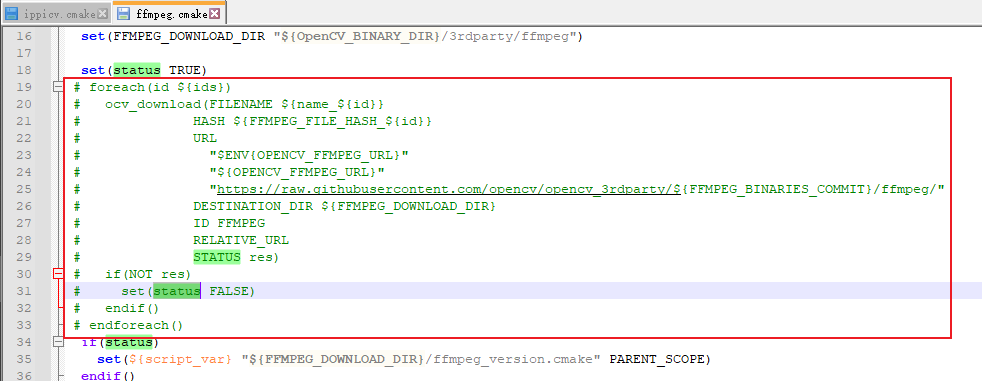
5.2.3. 打开opencv源码目录下的文件 /3rdparty/ippicv/ippicv.cmake 和 /3rdparty/ffmpeg/ffmpeg.cmake

注释掉以下部分：

重新开始cmake

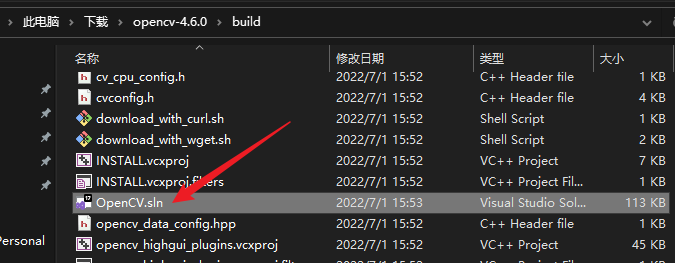
6. cmake结束后会在build目录下生成一个opencv的vs工程，用vs打开即可，然后再用vs编译。

图像的Hu矩

我们希望能用很少的几个特征代表一个图形，这些特征不因图形在图像中所在的位置、旋转角度、缩放比例的改变而改变，也不应受光照、噪点等影响。经过计算机视觉多年的发展，已经发现了很多这样的特征， 不变矩就是其中一个。

统计学中的矩

图像的几何矩

将图像的像素坐标看作是二维随机变量，像素的灰度值看作是概率，就可以套用统计学中的矩作为图像的几何矩。

原点矩：( M_{ij}=\sum_x \sum_y x^iy^jI(x,y)\ )

中心矩：( \mu_{ij}=\sum_x \sum_y (x-\hat x)^i(y-\hat y)^jI(x,y) \text ，其中(\hat x, \hat y)为图形的质心（重心）\ )

  1. 零阶矩 ( M_{00}=\sum_x \sum_y I(x, y) \text {，其中I(x,y)表示在(x,y)处的像素灰度值}\ ) 零阶矩计算的是所有像素灰度的总和，类比统计学中的概率总和
  2. 一阶矩 \( \\begin{cases} M\_{10}=\\sum\_x \\sum\_y xI(x, y) \\\\ M{01}=\\sum\_x \\sum\_y yI(x, y) \\end{cases}\\) 一阶矩计算出图像横纵坐标的加权和，权值即为该坐标像素。若想将权值归一化到（0，1）的区间，则可以将每个像素灰度值除以灰度总和，这样一阶矩就类似统计学中的数学期望了，该期望值是横纵坐标轴的加权平均值。该坐标点即为图形的质心（重心）坐标： \(\begin{cases} xc=M{10} / M_{00} \\ yc=M{01} / M_{00} \end{cases}\ )
  3. 二阶矩 ( \begin{cases} M_{20}=\sum_x \sum_y x^2I(x, y) \\ M{02}=\sum_x \sum_y y^2I(x, y) \\ M11=\sum_x \sum_y xyI(x,y) \end{cases}\ ) 类比上述统计学中的k阶原点矩
  4. 二阶中心矩 ( \begin{cases} \mu_{20}=\sum_x \sum_y (x-xc)^2I(x, y) \\ \mu{02}=\sum_x \sum_y (y-y_c)^2I(x, y) \end{cases}\ ) 即方差

Hu矩

中心距仅保证了平移不变性，若想要保证缩放不变性，则对中心矩归一化：

霍夫变换-线圆检测

假设笛卡尔坐标系中有n个点，每个点坐标为 ( (x_i, y_i)\ )，且这些点大致拟合成一条直线，问：如何找到这条直线？

霍夫空间

对于每个点 \( (x\_i, y\_i)\\) 都有无数条直线 \(y_i=kx_i+b\) 过该点。由k和b唯一确定该条直线，若将 \((k,b)\ ) 看作一个坐标，则该坐标点即为霍夫空间下的坐标。霍夫空间可以看作是原函数的 参数空间。

同理，对于过某一点的圆的方程 \( (x\_i-a)^2+(y\_i-b)^2=r^2\\) 其参数构成的点 \((a,b,r)\ ) 就是霍夫空间下的坐标。

有时，为了便于计算，会将笛卡尔坐标系转换为极坐标系进而得到极坐标系下的参数空间。

直线检测

在霍夫空间中 \( (k,b)\\) 方程可以表示为 \(b=-x_ik+y_i\) 也是一条直线。将所有n个点代入即可得到霍夫空间中的n条直线，若其中有m条直线相交于一点 \((k_m, b_m)\ )，对于这m条霍夫空间下的直线所对应的笛卡尔坐标下的m个点来说，它们有共同的k和b，即它们在同一条直线上，即检测出一条直线。对霍夫空间中所有直线的交点进行遍历就检测出所有的直线。进一步可以使用一些淘汰算法进行筛选及合并，减少多余的直线

圆检测

同直线检测，只不过将二维坐标系转换为三维。对于任意a、b，总能找到一个r，使得这三个参数构成的圆的方程过点 \( (x\_i,y\_i)\\)。\((a,b,r)\ ) 在霍夫空间中的图形如下：

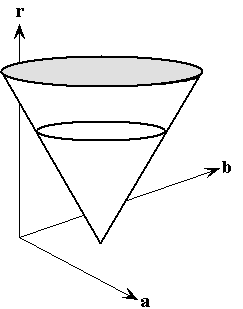
三个锥面相交即确定一个参数坐标点，进而得出经过这三点的圆的方程。

对 HoughCircles 方法中参数dp的理解

该参数可以理解为拟合精度，或者去除多余圆的程度。

简单理解为将霍夫空间的一个面（或一个空间等）划分为多个小格子，处于同一个格子的点视为一个点。dp即为每个小格子的宽度。dp=1 代表每个小格子仅代表一像素，即不进行合并。

例如，在霍夫空间下，有3个锥形，其中两个相交，第三个并没有过这个相交线，但该线与第三个锥面的最近距离小于2。此时，如果设置 dp=1 就检测不出圆形，因为并没有相交点。但如果设置 dp=2 则意味着所有小于2的距离将视为同一个点，此时就能检测出一个圆。

图像傅里叶变换

一维函数 f(x) 的傅里叶变换：

任何周期函数都可以通过多个正弦波的叠加表示

图像（二维函数）的傅里叶变换有两种理解方式：

  1. 任何图像 f(x,y) 也都可以由无数个正弦波平面叠加而成，他们具有不同的 频率、相位、振幅、方向 四个属性
  2. 对图像的每一行每一列做一维傅里叶变换

图像的傅里叶图谱：

  1. 可以根据傅里叶图谱还原图像
  2. 傅里叶图谱只能表示频率、方向、振幅三个属性。图谱中的每个点相对于中心点的位置就对应正弦波平面的方向，每个点的灰度值代表的就是振幅。为什么没有相位信息也能还原？
  3. 傅里叶函数具有中心对称性，所以傅里叶图谱左上和右下、右上和左下的图像是中心对称的
  4. 傅里叶图谱中每个点代表的是一个正弦波平面的函数，即一个M_N的图片可以转换为M_N个正弦函数叠加
  5. 傅里叶图谱中每个点所代表的正弦波频率从左到右增大，但由于中心对称性的缘故，图谱中越靠近中心点所代表的频率越高，边缘代表的频率较低。为了方便观看，一般通过 ffshift() 函数将频率低的点和频率高的点调换位置，即傅里叶图谱中越靠近中间的点的频率越低
  6. 可以将正弦波频率理解为图像梯度，频率越高，图像的变化越剧烈。所以高频往往代表了图像中的噪音和边缘

参考：

https://zhuanlan.zhihu.com/p/99605178?utm_source=qq

https://blog.csdn.net/weixin_46233323/article/details/105355133

https://www.zhihu.com/question/355013340

https://homepages.inf.ed.ac.uk/rbf/HIPR2/fourier.htm